Liegedreirad - theoretische Details

1 Die Fliehkraft

Bei einer kreisförmigen Bewegung wie dem Durchfahren einer Kurve wirkt auf den bewegten Körper eine Fliehkraft Fz senkrecht zum Kreis nach außen (Abb.3).

geg.: Masse m , Geschwindigkeit v , Kurvenradius am Schwer-

punkt r0

Fz = m * vý/r0

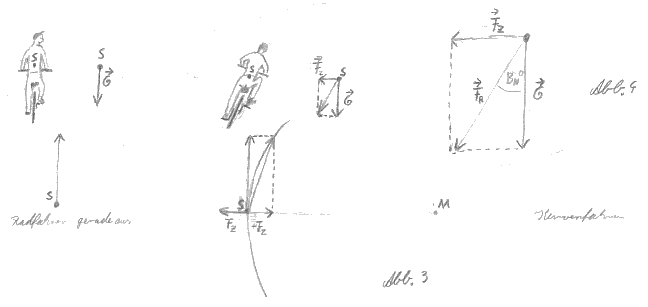
2 In die Kurve legen

Damit diese Kraft ein Fahrrad nicht umkippen läßt, "legt sich der Fahrer um den Winkel Bnø soweit in die Kurve", daß der Vektor der resultierenden Kraft aus Fliehkraft Fz und Gewichtskraft Fg wieder in Richtung des Fahrradrahmens liegt (Abb.4). Entlang des starren Rahmens kann nämlich durch diese Kraft der Schwerpunkt nicht relativ zum Auflagepunkt des Rades verschoben werden. Das Gleichgewicht bleibt also stabil.

geg.: Geländeneigung senkrecht zur Fahrtrichtung H`ø ,

Erdbeschleunigung g

Fg = m * g

a = sin H`ø * Fz

b = Fg - a

c = cos H`ø * Fz

tan Bnø = c / b

Fz in a,c; a,Fg in b; b,c in tan Bnø eingesetzt;

m weggekürzt :

tan Bnø = (cos H`ø * vý/r0) / (g - sin H`ø * vý/r0)

1 Wann kippt das einfache Dreirad ?

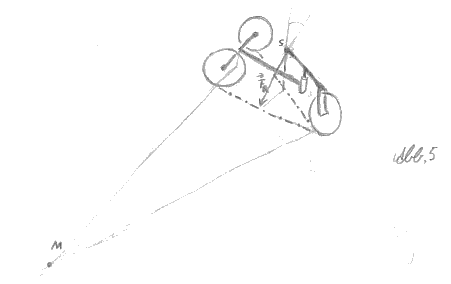
Ein einfaches Dreirad (Abb.1) kann sich nicht "in die Kurve legen". Es bleibt vielmehr eine Art gedachte "Kipplinie" zu beachten, auf der das Dreirad bei einer evtl. zu großen Fliehkraft Fz nach außen kippt (Abb.5). Kennt man den Winkel Bnø, in dem die Resultierende aus Fliehkraft Fz und Gewichtskraft Fg wirkt, sowie die Höhe des Schwerpunkts hs` , kann man den nötigen Abstand bn zur Kipplinie errechnen, den der Schwerpunkt S umbedingt noch haben muß, soll das Rad nicht kippen (Abb.6).

geg.: hs` (Siehe unten !) entspricht zunächst der ursprünglichen Höhe des Schwerpunktes hs

bn = tan Bnø * hs` / cos H`ø

Es gibt Möglichkeiten, sich ein Dreirad doch in die Kurve legen zu lassen:

2.1 Kurvenleger aufgrund einer waagerrechten Achse

Eine Weg zum Bau eines Kurvenlegers ist, neben der normalen Lenkung auch noch eine horizontale Achse anbringen, um die der Schwerpunkt zur Seite kippen kann.

2.2 Kurvenleger aufgrund der Lenkung über eine Starrachse - DREIRAD ALS KURVENLEGER

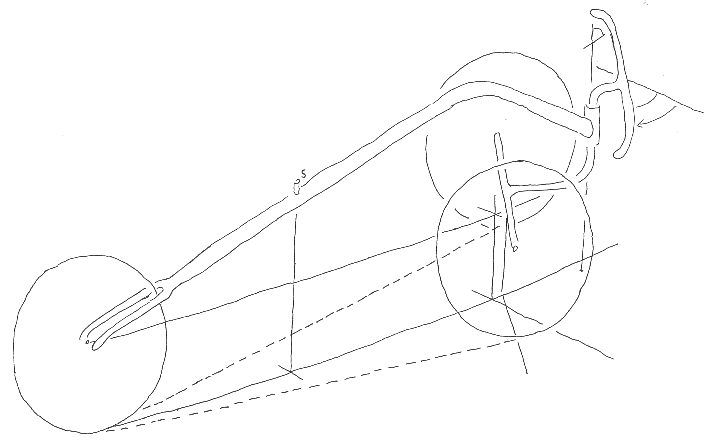
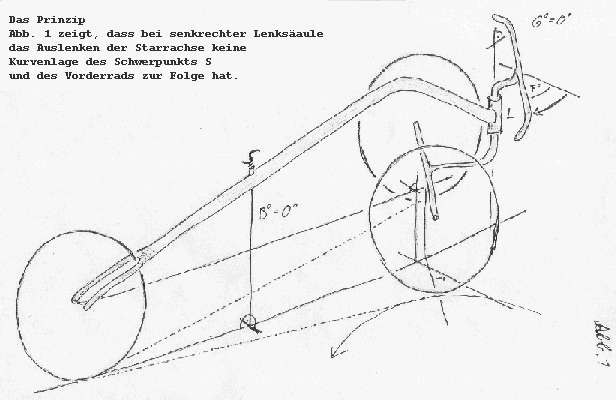
Man betrachte ein Dreirad, dessen beide Räder der äußeren Spuren um eine einzige Achse ausgelenkt werden, um eine Kurve zu fahren (Drehschemellenkung). Ist der Winkel zwischen Boden und Lenkkopflager Gø (Steuerkopfwinkel) 90ø, so bewegt sich das Rad beim Lenken ausschließlich auf einer horizontalen Ebene zur Seite (Abb.7). Wenn der Winkel Gø jedoch kleiner gewählt wird, kann man die Drehbewegung beim Lenken in der Ebene senkrecht zur Lenkachse (Aø) als eine Kombination aus einer Bewegung in horizontaler Ebene (Fø) und einer anderen auf vertikaler Ebene (senkrecht zur Ebene der Lenkachse) (Bø) beschreiben.

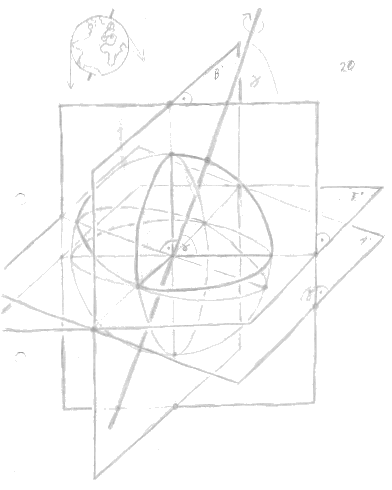
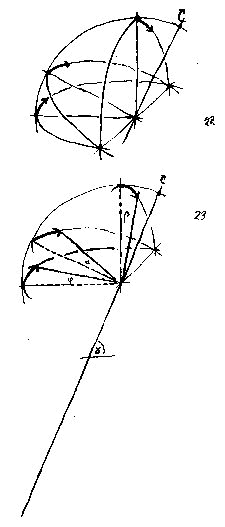
Genauso könnte man das Drehen eines Globus um eine schräge Achse als eine Kombination aus einer Bewegung parallel zur Tischplatte, auf der er steht, und einer anderen verstehen, die senkrecht zur Tischplatte und der Ebene der Globenachse liegt (Abb.10,20-24).

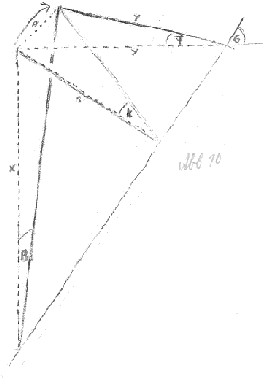
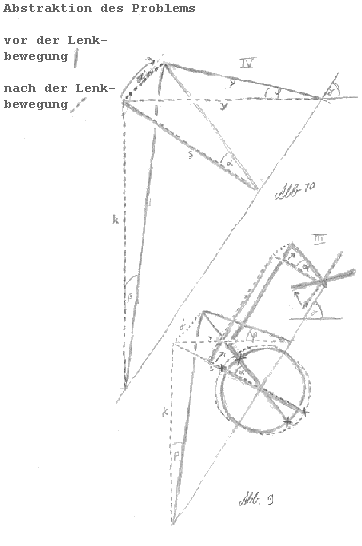
Das Drehen mit den Winkel Aø um eine Achse im Winkel Gø zur Waagerechten faßt man als Drehen um den Winkel Fø in horizontaler - und um den Winkel Bø in vertikaler Ebene (senkrecht zur Ebene der Lenkachse im Winkel Gø zur Waagerechten) auf (Abb.9).

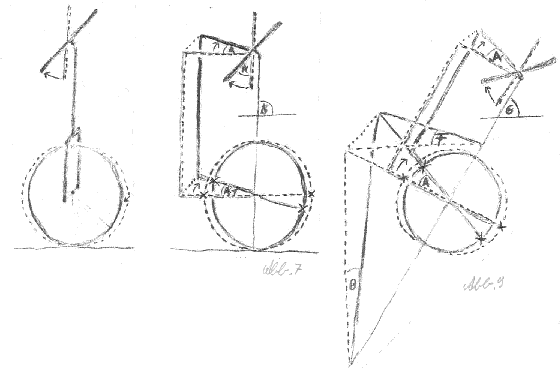
Die Bewegung des Rades in waagerechter Ebene (Fø) enspricht der Auslenkung auf der Ebene des Bodens, bestimmt also beim Fahren den Kurvenradius. Das Rad macht dabei aber auch eine Bewegung auf jener vertikalen Ebene (Bø), eine Art Kippbewegung senkrecht zur Fahrtrichtung, der obere Teil des Rades neigt sich zur Seite. Wenn nun die Hauptmasse (Fahrer) mit diesem Rad verbunden ist, führt der Schwerpunkt S beim Auslenken des Rades -also beim Kurvenfahren- eine ähnliche Bewegung Bø relativ zum Auflagepunkt des Rades z.B. ins Kurveninnere aus. Ein Dreirad mit derartiger Lenkung legt sich also in die Kurve (Abb.2). Nochmals:

Ist der Winkel zwischen Boden und Lenkkopflager Gø (Steuerkopfwinkel) 90ø, so bewegt sich das Rad beim Lenken ausschließlich auf einer horizontalen Ebene zur Seite (Abb.7). Wenn der Winkel Gø jedoch kleiner gewählt wird, kann man die Drehbewegung beim Lenken in der Ebene senkrecht zur Lenkachse (Aø) als eine Kombination aus einer Bewegung in horizontaler Ebene (Fø) und einer anderen auf vertikaler Ebene (senkrecht zur Ebene der Lenkachse) (Bø) beschreiben.

Genauso könnte man das Drehen eines Globus um eine schräge Achse als eine Kombination aus einer Bewegung parallel zur Tischplatte, auf der er steht, und einer anderen verstehen, die senkrecht zur Tischplatte und der Ebene der Globenachse liegt (Abb.10,20-24).

Das Drehen mit den Winkel Aø um eine Achse im Winkel Gø zur Waagerechten faßt man als Drehen um den Winkel Fø in horizontaler - und um den Winkel Bø in vertikaler Ebene (senkrecht zur Ebene der Lenkachse im Winkel Gø zur Waagerechten) auf (Abb.9).

Die Bewegung des Rades in waagerechter Ebene (Fø) enspricht der Auslenkung in Ebene des Boden, bestimmt beim Fahren den Kurvenradius. Das Rad macht dabei aber auch eine Bewegung auf jener vertikalen Ebene (Bø), eine Art Kippbewegung senkrecht zur Fahrtrichtung, der obere Teil des Rades neigt sich zur Seite. Wenn nun der Schwerpunkt S mit diesem Rad verbunden wird, führt er beim Auslenken des Rades -also beim Kurvenfahren- auch diese Bewegung Bø relativ zum Auflagepunkt des Rades z.B. ins Kurveninnere aus. Ein Dreirad mit derartiger Lenkung legt sich also in die Kurve (Abb.2). Wie weit legt sich nun dieser Kurvenleger durch Lenken jeweils in die Kurve?

j = sin (Aø/2) * 2 * s (Abb.11)

= sin (Bø/2) * 2 * k (Abb.12)

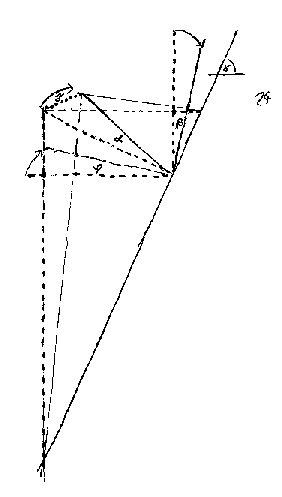
s = cos Gø * k (Abb.14)

j = sin (Aø/2) * 2 * s = sin (Bø/2) * 2 * k

s eingesetzt, durch 2, k dividiert:

sin (Aø/2) * cos Gø = sin (Bø/2)

j = sin (Fø/2) * 2 * y (Abb.13)

s = sin Gø * y (Abb.14)

j = sin (Fø/2) * 2 * y = sin (Aø/2) * 2 * s

s eingesetzt, durch 2, y dividiert:

sin (Fø/2) = sin (Aø/2) * sin Gø

k = tan Gø * y (Abb.14)

j = sin (Fø/2) * 2 * y = sin (Bø/2) * 2 * k

k eingesetzt, durch 2, y dividiert:

sin (Fø/2) = sin (Bø/2) * tan Gø

2.2.1.1 hs`:

Die ursprüngliche Höhe des Schwerpunktes hs wird dabei - sollte sich der Schwerpunkt um Bø neigen - zu hs`, also kleiner (Abb.18).

hs`= hs * tan Bø

hs` in bn eingesetzt:

bn = tan Bnø * (hs * tan Bø) / cos H`ø

tan Bnø in bn eingesetzt:

bn = [(cos H`ø * vý/r0) / (g - sin H`ø * vý/r0)] * (hs * tan Bø) / cos H`ø

2.2.1.2 rø:

Der Radius in dem sich der Schwerpunkt S bewegt wird durch das "in die Kurve legen" kleiner.Der Winkel Yø zwischen den verschiedenen Kurvenradien von Schwerpunkt r0 und Rädern rn muß bekannt sein,

um r0 zu finden (Abb.15).

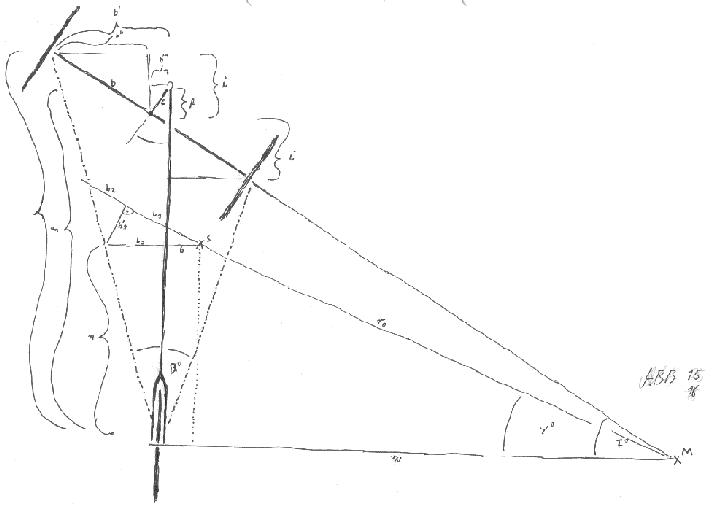
geg.:Strecke zwischen Achse des ersten Rades und der der

beiden anderen m ,

Strecke zwischen der Mitte der beiden Hinterräder und der

Lenkachse c ,

Kurvenfahrwinkel Fø

o = sin Bø * hs (Abb.18)

f = c / cos F`ø

rn = (m - f) / tan F`ø

tan Yø = n / (rn - o)

f in rn ; o,rn in tan Yø eingesetzt:

tan Yø = n / [(m - c / cos F`ø) / tan F`ø

r0 = n / sin Yø

Dies neue r0 müßte nachdem auch Yø eingesetzt wurde nun in die Formel für bn eingesetzt werden.

2.2.1.3 bø:

Der tatsächliche Abstand b0 des Schwerpunktes zur Kippachse wird beim Kurvenlegen größer. Um dies zu berechnen, muß zunächst der Winkel Dø zwischen dem "Kiel" ( Mittellinie beim Geradeausfahren, Linie durch das einzeln stehende Rad und dem Lenkkopflager ) und der Kipplinie in einer bestimmten Kurve gefunden werden.

geg.: halbe Strecke zwischen den beiden Hinterrädern b

b" = cos F`ø * b

b"`= sin F`ø * c

b` = b"` + b" (Abb.16)

i = sin F`ø * b

c` = cos F`ø * c

tan Dø = b`/ (m + c` - i)

b"`,b" in b` ; b`,i,c` in tan Dø :

tan Dø = [(cos F`ø * b) + (sin F`ø * c)] / [m + (cos F`ø * c)-

sin F`ø * b)]

h` = sin Yø * (bs + o)

bs = tan Dø * n

b1 = cos Yø * (bs + o) (Abb.15)

b2 = h` * tan (Yø + Dø)

b0 = b1 + b2

o in b1,h` ; h` in b2 ; bs in b1 ; b1,b2 in b0 :

b0 = cos Yø * (sin Bø*hs + tan Dø*n) +

tan (Yø+Dø) * [sin Yø *(sin Bø*hs + tan Dø*n)]

Es könnte theoretisch hier auch noch Dø und Yø eingesetzt werden

Damit das Dreirad nicht umkippt, muß natürlich der tatsächliche Abstand des Schwerpunktes von der Kipplinie b0 (durch das Kurvenlegen vergrößert) mindestens so groß sein wie der nötige bn. Die Formeln für den nötigten und den tatsächlichen Abstand des Schwerpunktes zur Kipplinie bn und b0 können gleichgesetzt werden, möchte man immer so fahren, daß das Dreirad nicht kippt. Gelänge es, sie nach Bø (Winkel in dem sich der Kurvenleger neigt) aufzulösen, könnte man aus diesem Bø und dem der Kurve entsprechenden Fø (Winkel in dem in Ebene des Bodens gelenkt wird) [hierzu Formel für r0 nach Fø aufzulösen] exakt die jeweils ideale Neigung des Lenkkopflagers Gø errechnen

[ tan Gø = sin (Fø/2) / sin (Bø/2) ].

(Als Vereinfachung wird hier jedoch zunächst gesetzt, daß Bø geauso groß wie Bnø sein soll. Außerdem wurde die Formel für r0 mit der einfacheren für rn ausgetauscht, um sie nach Fø aufgelösen.

Bnø = Bø

sin F`ø= -[rn*c/(rný+mý)]+ wurzel[rn*c/(rný+mý)ý-(cý-mý)/(rný+mý)]

Hierbei stellt man fest, daß das ideale Gø zwar bei verschiedenen Kurvenradien in weiten Bereichen gleichgroß bleibt, aber bei verschiedenen Geschwindigkeit variert.)

2.2.2.1 Grenzen beim Kurvenfahren

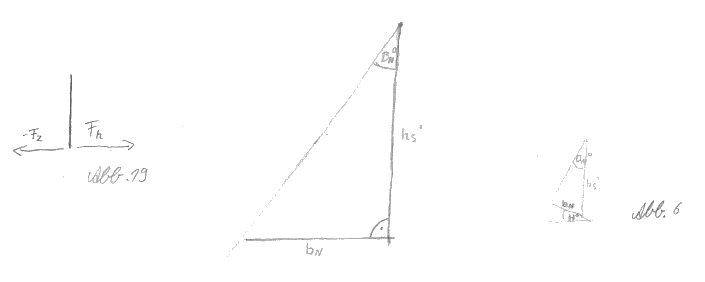
Durch die beschränkte Haftreibungskraft Fh der Reifen auf dem Untergrund, die der Fliehkraft Fz entgegenwirkt, bleibt das Risiko nach außen wegzurutschen (Abb.19). Trotz der Möglichkeit, sich in die Kurve zu legen und daher nicht nach außen umzukippen, kann also nicht jede Kurve beliebig schnell zu durchfahren werden.

geg.: Haftreibungszahl fh

Fh = fh * m * g

Jeweils die Formeln für Fz und Fh gleichgesetzt; eingesetzt:

Fh } Fz

fh * m * g } m * vý / r0

m rausgekürzt:

vý/r0 { fh * g

nach v bzw. nach r0 aufgelöst:

v { wurzel[ fh * g * r0]

r } vý / (fh * g)

vý/r0 bezeichnet die Kurve und die Geschwindigkeit, bei denen man gerade noch nicht nach außen wegrutscht, nicht "aus der Kurve fliegt".

Wie groß muß der nötige Abstand des Schwerpunktes eines Rades zur Kipplinie bn bei dieser extremsten Kurvenfahrt sein? Um welchen Winkel Bø muß sich das Rad hier in die Kurve legen?

statt vý/r0 fh*g in bn eingesetzt:

bn max. = [(cos H`ø * fh * g) / (g - sin H'ø * fh * r0)] *

(hs * tan Bø) / cos H`ø

Durch Einsetzen von fh * g für vý/r0 in die Gleichung Bn kann man ein maximales Bnø ermitteln. Ordnet man diesem Bnømax wieder Geschwindigkeiten v und Kurvenradien r0 zu, erhält man wie durch die Formel für r0 (aus II.2.2.2.1 "Grenzen") die extremen Kurven, die gerade noch mit der gegebenen Geschwindigkeit durchfahren werden können.